�۹��
�磌�z�w�ߪ�����
�ɮɾA�Ρ]�j���^
�{�b�Ǫ��w�ߡA�H�ᤣ��ΡH
�B�B�A�Ρ]���~�^
�X��d�ǾǪ��A�^�곺����ΡH
�b�B�ʤ��]��H
�@�w����A���M�b��������|�^�ˡ]���O�R�̫��R�ܡH�^�]�����B�ʡ^
�Ϥ�����A�������U�]���ߤO�^�Fī�G�|���U�ӡ]�U���ޤO�^�A��y�����|�H�]����B��ʡ^
�h�@�B�A�����S���B�ʡ]�Y�R��^�ɾA�Ϊ��W�h�@���z�w�ߡH
���A����s�� "�R��"�H
�p�G�S�k�w�X���@�ӵ����R��y�Шt�A�h�h�ӨD�䦸�A�Ʊ� (1) �F�ѦP�@���z�w�߾A�Ρ]���z�{�H�����{�i�H���P�^���@�t�C�ѦҮy�СC�åB (2) ���P�ѦҮy�Ф������{�H�A�ڭ̤]�i�H��T�ഫ�A�]�N�O���A���D�@���y�Шt�����{�H�j�p�A�i�H�w���P�@�ƥ�b�t�@�Ӯy�Шt�Q�[��쪺�j�p�C
������Y����Ӥ������R��y�Шt�A�̲ŦX�P�@���z�w�ߪ��n�D�H
�շQ f = ma�Aa �O�[�t�סA����m��ɶ����G���L���A�y�Шt�����L�۹�[�t�ס]�Ȭ۹�t�ס^�̡A���ӷ|�ݨ�P�˪� f = ma �����A�o�i�H�q x'(t) = x(t) + v t ���ഫ�A�|���X�@�˪� a �ӤF�ѡC
�D�ʮy��
�D�ʮy�Шt�G�N�����[�t���y�СA���t���ʪ��y�Шt����O�C
�@�Ӧ��Ϊ����z�w�ߡA�O�㦳�b�D�ʮy�Шt���ഫ�����ܩ� (invariance) ���C�Ҧp���y�B�ʩw�ߤ��� f = ma �A ���ޭn�� x ���y�Шt�٬O x' ���y�Шt�Ӫ��ܡA�u�n���̳��O�L�[�t�ת��D�ʮy�Шt�A�]�N�O�� x �P x' ���������Y�O��x = x' + vt �A�h f = ma �� f' = ma' �o�˪��Φ��b����D�ʮy�г��O�@�˪��]�j�a�i�H�ۤv�N�N�ݡ^�C
�] Maxwell ��{����y�w�߱ߤF200 �~�A ����Q���� 300 �~�C �^
���Q���P���y���ɶ��P�Ŷ�
����A�b�D�ʮy�Шt�����A�P�ɶ��B�Ŷ����������z�q�p���ഫ�H�H�t�ץH�ҡG
������p�ɳt���Q�����B���W�����R�b���[�����ʦ�m x'�A�h���ȹ�a���t�ɳt v �A����a������m x �i�Q���ܬ�
x_ground = x_train + v_train * t
������p�ɳt���Q�����B���W���ȦV�e�H�y�t�G�Q�������Y�βy�A�h���a���Ө��y�t�O�ɳt�C�Q�����C�t�|�ۥ[���o�^�ơA�Y�q�g���������צӨ��A���ɹL�{�p�U�G
x_ball_ground = x_ball_train + v_train * t
�䤤
x_ball_train = x_ball_train_0 + v_ball_train * t
�W���N�J�W�W���o
x_ball_ground = x_ball_train_0 + v_ball_train * t + v_train * t
�t�v�O��m�H�ɶ��ܤ�
v_ball_ground = d x_ball_ground/dt = 0 + v_ball_train + v_train
= v_ball_train + v_train
�]�N�O��
70 = 50 + 20
�o������n��Ǫ��H
���D�O�A�H�W��k�O�ھ� x = x' + vt �����A�Ӥ��O���窺���G�C�]�ڭ̱N�|�ݨ�A�Y�϶i�����A�u�n v ���p (����s���p�ݷ|����) �A�o�Ӥ����]�O�諸�A�H�����Ӧ����t���ʪ��g��C�^
�q�B�ϻP���J���º���{��
�q�ϾDZq�̦����w�۩w�ߡ]�R��q���q�B�O�B�Z�������Y�^�B�찪���w�ߡ]�q���p��b�Ŷ����إ߹q���^�B�H�Φw���w�ߡ]�T�w�q�y���ͩT�w�ϳ��^�B�k�Բĩw�ߡ]�ܤƪ��ϳ��ɭP�q�y���͡^�A�̫�A�Ѱ��J���º��ޤJ�첾�q�y�Ӿ�X�����R���|���@�դ�{���A
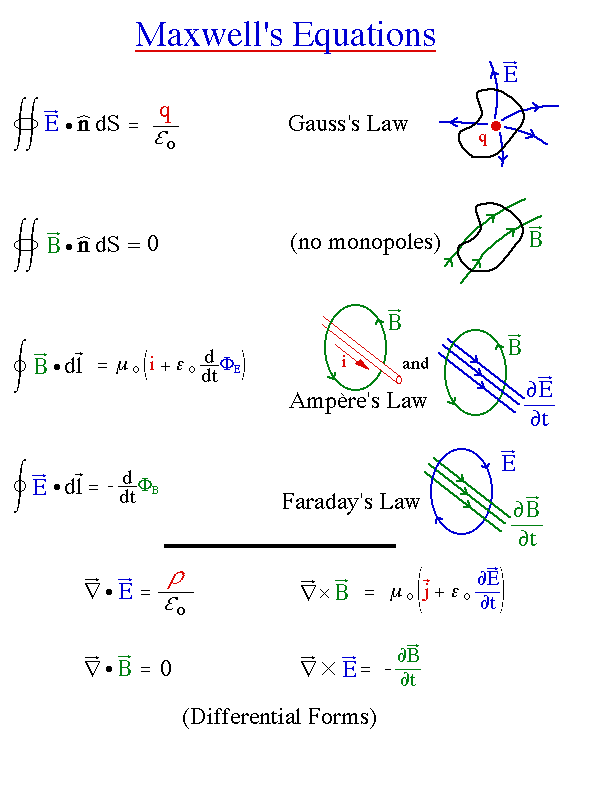
�q�ƾǧΦ��W�i�D�ڭ̹q�P���H�ɶ����ܤƷ|�Φ��i�ʡA�B�i�t�O�T�w���`�ƭȡA��]�p�U�G

�W���o�ӹ�ɶ����L���⦸�B�o�ӪŶ��]���L���⦸����{���A�㦳�i�ʤ�{�����S�x�C�i�t���誽���X�{�b�Y�Ƥ��A���B�C�A�t�ۥ[������~�~�T�{�L�~�A���q�Ϫi�|�����u�H
���J���º���{������b���P�D�y�Шt���ä��㤣�ܩʡH�Y�p���n�γo�Ӥ����ٱo�������O�n�Φb���@�ӰѦҮy�Шt�A���ӥi��a�H���O�A�Y���㤣�ܩʡA�h�q�Ϫi�b����D�ʮy�Шt���O�T�w�ȡA�u�O���i��ij�C
�|���|�]���O�i�Ӥ��O�ɤl�A�t�צb���P�D�ʮy�Шt�������ഫ��N���O�Υ[���H��ꤣ�|�A���j�媫�z�A���P�[��̡A��i���S�ʪ��y�z�i�ѳ��R�Ǥ����o��C
���R���n�Ǥ����P Maxwell �����������t
�a��������í��W�ܰ��A���������ܧC�A�o�O�]���n������n�C���Ů�@�۹�B�ʪ����G�C�W�v�����p�U�G
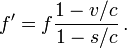
�䤤 v�Bs�Bc ���O�Oť�̡B�n���A�Ϊi���t�סC
��M�H�ӡ]�q�Ϫi���Ǽ��C���^
���J���º��@���{�����@�ضǼ��q�Ϫi���C���A�p�P�Ů𤧩��n���H�Τ���������i�@�ˡC���̤j�����D�O�A�[���������������C
�ɥR�G���t�q�������v
Fizeau ����
���t�b���褤�O�C�U�Ӫ� c / n�AFresnel �{���y�ʤ���|�i�@�B �����a �v�T�q�L�������������t�C�L�{���P��V���ʤ���]�p�y��^�������t�|�O
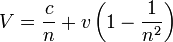
�Ӥ��O V = c / n + v �A�o�˥L�~���������a���P�H�Ӧ��G�O�R��A�������A�O�]�� �W���A���ت� 1 - 1/n2 �]�Y�ҿת� Fresnel �즲�Y�� (drag coefficient)�^ �ܤp�A���ӥ[�W���y�t v �������~�S������줶�褤���t c / n �W �C �]�t�~�A�u�Ū���g�v n = 1�A�@������U�Ů𪺧�g�v n = 1.0003�C�^
1851 �~ Fizeau �Τz�A���P��ȥb�z���i��F�H�U���� (�Ԩ�����ʬ�, 2)�A�� " �L�� "�]�� 10% �~�t�A�� �ѦҸ���^�F Fresnel �����Q�A�L�u���q��F�W��
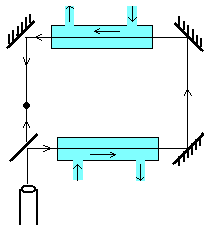
�[���ܷN��
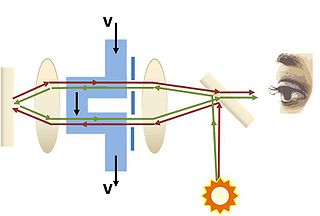
�˸m�ܷN��
�b���ɡA�����G����F�H�Ӫ��s�b�C�]�Ъ`�N�A����èS���q���C�ƹ�W�ᦳ Lorentz (1895) ���X���K�������A�� Zeeman (1914) �ҹ�C�q��@�����ݨӡA���ѧڭ̧����i�H�Ѭ۹�רӲz�ѳo�Ӳ{�H�C�^
�ڥi�ˡв��Q (Michelson-Morley) ���ɭP�T�w�����t���w����]���H���o�̦��W�����ѹ���^
1887 �~�A
�i�������i���i���D�`�u�]3000 �J�� 7000 �J�^�A���t�]�ܧ֡A�]���t�@�I�I�Z���N�i�H�b�z�A�����W�ݥX�ӡC�a�y������Τ���A�Y�H�Ӧb�t�z���O�R��A�h�a�y�蠟���۹�B�ʡC���M�٬O���H�h�æa�y�P�H�ӥi��Q�a�y�a�ۨ��A���j��@�ˡC���o�Q�k�èS�ണ�Ѧ��i�@�B�ҩ��άO���Ҫ����|�]�M��۹�׳Q�����ҹ��A�H�Ӫ����s�b�]�N�w�פF�^�C
�N�W�A�ڥi�˻ݭn�P�@����l�]�P�ե��^�����۫�������Ӥ��P���|�C
Michelson-Morley ����˸m�p�U�G
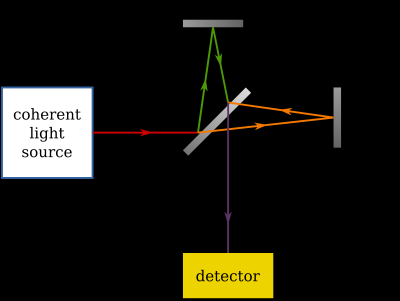
���u�U�� 11���ءA�H�j�z�۬����y�A�˸m�B�b���ȤW�H��A�P�ɤ]�i�H��ʡC
�����窺���R
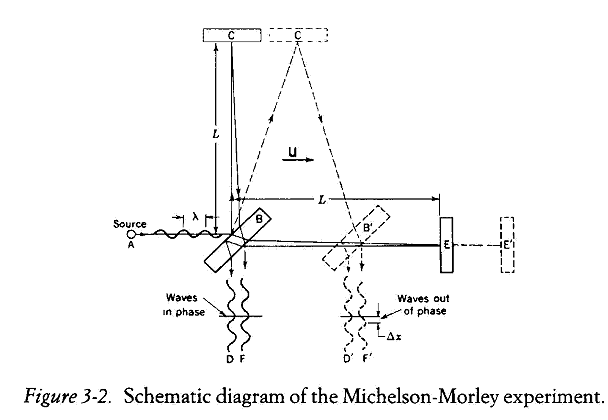
����R�p�U�Gp1, p2, p3
���O�G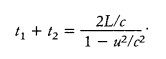 ��
�� 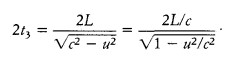 �A���̬O���@�˪��C
�A���̬O���@�˪��C
"�S���ҭۯY�A�N�S���۹��" -- �R�]���Z
���F�����W�z�H�ӹ�����G�a�y���L�۹�t�W�[�����I�A�ҭۯY�������X�H�ӷ|�������Y�u������
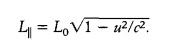
�p�G���O�u���A�h�M�Φb�W�z M-M ���窺���G�W�ɡA�N�|��
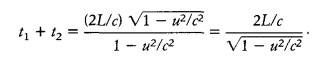
�h���u�����G�N�u���@�ˤF�C
�A�i�H�Q���A���ɤ]���H�{���o�@�k�ӤH���F�B���۵M�A���O�v�y���@�k�C
�R�]���Z���X���۹�פ��]
�D�ʮy�Ф����z�w�ߧΦ�����
�Ҧ��D�ʮy�Ф����t���w
�w�i ���n���s�[���G�u�P�ɩʡv�O�۹�Ӥ��O���諸
�P���y�B���Q���ɪ��[�ܤ��P�����G�O�A�b�۹�פ��U�S�� "�P�B�ɶ��y" �o�@�^�ơA�]����Өƥ�O�_ "�P��" �o�ͬO���M���[��̪��۹�t�ת��A�A�ӫD���諸�C
�]�H�U�A�ڭ̭n�}�l���\�w�q t �P t' �����P�^
�q �R�]���Z�۹�� �ɥX �ҭۯY�ഫ
�]�H�U�ڭ̨ӬݬݡA��˱q�R�]���Z���۹�פ��]�A�ӾɥX �ҭۯY�ഫ�^
(a) ����ܪ��O�@�Ӱ{�����˾��աA�H�Ϋ�����B�ʤ�V�T�w�Z������l�C��ո˸m��b���W�A���V�k�H u ���t�v���ʡC
�b���ॢ�@��ʪ����p�U�A�O�a���w��̪���m�]�]�N�O�X�o�I�B�^�O�b x = 0 �C
�P�ˤ@�� "�{���B�Ϯg�B����" ���L�{�A�H���[��̬ݨ쪺�O (a) �Ь� primed (S') system�F�Ӧa�� �[��̬ݨ쪺�h�O (b) �Ь� un-primed (S) system
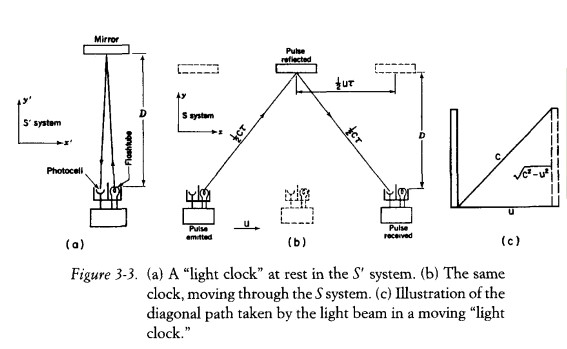
�{�b�A�H���[��̶q�o��L�{�ɶ� t' �A�L�n��˴���X�a���[��̶q�o��L�{�ɶ� t �H
�Q�Ψ�Өt�Ϊ����t�O�@�˪� �]�۹�פ��]�^
c' = 2D / t'
c = 2 √[D2 + (ut/2)2] / t
c' = c
�Y�o��
2D / t' = 2D √[1 + (ut/(2D))2] / t
t' = t / √[1 + (ut/(2D))2]
�o���٦� D�A���L�S���Y�AD2 = (ct/2)2 - (ut/2)2�A�Y (2D)2 = (ct)2 - (ut)2
�]���W���� (ut/(2D))2 = u2t2 / (c2t2 - u2t2) = u2/ (c2 - u2)�A�Y
1 + (ut/(2D))2 = 1 + u2 / (c2 - u2) = (c2 - u2 + u2) / (c2 - u2) = c2 / (c2 - u2) = 1/ [1 - (u/c)2]
t = t' / √[1 - (u/c)2]
t = t0 / √[1 - (u/c)2]
�٦��A�]�i�H�o�˱�
2(ct'/2) = 2D
=> ct' = 2D
2 ( ct/2 ) = 2 √[ D2 + u2 (t/2)2]
=> c2t2 = 4D2 + u2t2
=> (c2 - u2) t2 = 4D2
=> √[c2 - u2] * t = 2D
�G
ct' = 2D = t * √[c2 - u2]
=> t' = t * √[1 - (u/c)2]
=> t = t' / √[1 - (u/c)2]
�]�S�t�@�ر��ɪk�^
����R��y�Шt�����[��̬ݰ_�ӡA���������|�O����A�������Y�O�P�����������Ӥ�A�����t�T�w��h�A�O c : u ����ҡA�]�N�O���A�]���w�z�^�P�����䪺���פ�ҬO c : sqrt( c2 - u2) �C�{�b�R���[��̴������[��̷Q�A�o�D���b���ʮy�Шt���������O c ��Ҫ����ӬO sqrt( c2 - u2) ��Ҫ����A�ӥ��u�o�g�찻���@�ˬO�n���� dx2 - c2t2 = 0 �����p�U�A�ߦ� (�R���[��̻{�������[��̪�) �����ܺC�C
sqrt(c2-u2) t = c t'
t = t' / sqrt[ 1-(u/c)2 ]
���n���� : ���u�Ŷ��y�Эn�ഫ �A�ɶ����]�n�C
�P�ɩʬO�۹諸
�d�� : ���[�����I�V�e��P�ɵo�y ���W�[��̻{�� �P�� ��F�A�a�� �[��̻{�� ���P�� ��F�C(��L����������Ҥl�٫ܦh)
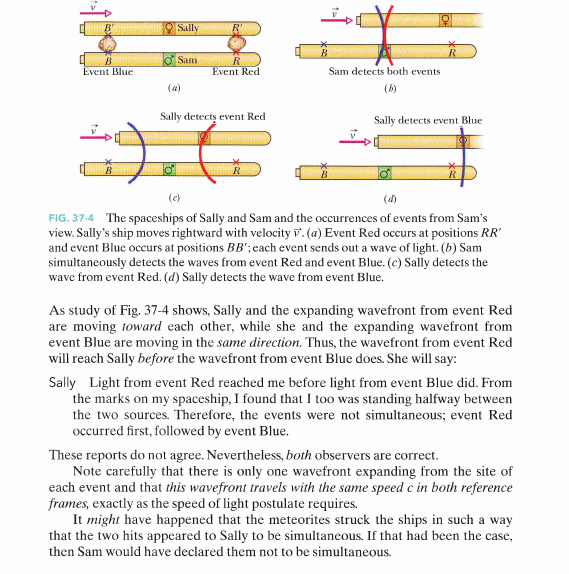
���ǹL R�A ���D�]���B�a�A�Y�i���q
���s���ɪŻR�x : �y�СB���סB�ɶ��B�t�ۥ[�B��ब��
�b�R��[��̬ݨӡA�b�ʪ�����Ψt�η|�G
�����Y�u
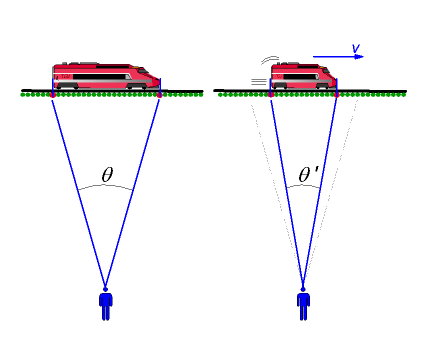
�p����q�B���骺���סH
�Щw�Y���A�O���ɶ��t�C�Y���Z�� = ��ʳt�v × �Y���ɶ��t
�����Y���� ����
�X�ӯU�q�۹�����Y�q�i�@�B�� ����
ù�ҭۯY�ഫ������ �P �ɪŶ��Z���ܩʪ��ҩ�
�ɶ����� (Time Dilation)
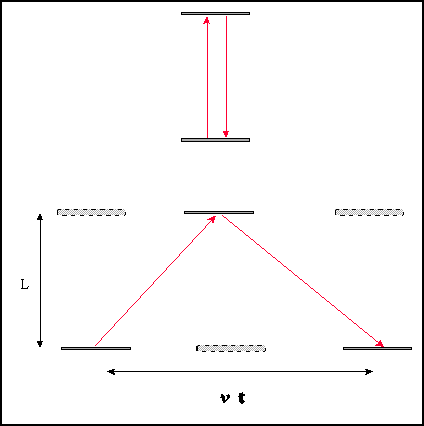
�Q�β���w�z�A�û{�w���b����D�ʮy�г��O�P�@�ӭ� c �C
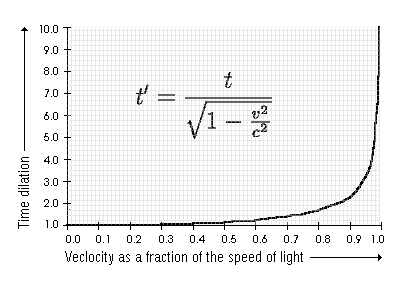
(�� : �W�Ϥ��� t �Y t0 �]�N�O�W�@�`���l�� t' )
��q�W�[
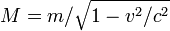
�]�@�DZM�a�D�i�u�� "�R���q" �P "�۹�B�ʤU���ʶq"�A�קK�ͳo���H�t�ק��ܤ��ͬ۹��q�C�^
�۰����A�պ⪺���� http://hyperphysics.phy-astr.gsu.edu/hbase/relativ/tdil.html
�t�ۥ[����
�R�]���Z���ɥX
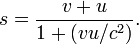
���O����Q����
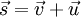
�䤤 c �O���t�C
��ब��
E = m c 2
���������ɡA�n�q�ʶq-��q���Y
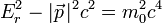
�Ҽ{�X�o�A�ԽФU�G
�]�@�����U�A�Q�� ��q�P��q����O���ġB�ब�����Ϲ��A���R�]���Z�������Үɪ���Ҧ�������ɡA�Q�Υ��l�A�� �s���^
�y���ഫ
�ҭۯY�ഫ (�{�i�Ҵ��� �ഫ)
�p�W�z�A������Ǯa �ҭۯY �b���H�Q "�ץ�" ���J���º���{�����ŦX���Q���ഫ�ɡA�o�{�F�ΤU�C�覡�եh�ഫ�]�ഫ��Ӥ��P���D�ʮy�Шt�[��̩Ҵy�z���ƾڡ^���ܡA ���J���º���{���i�O����Ӫ��Φ��G
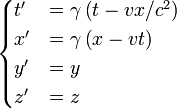
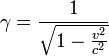
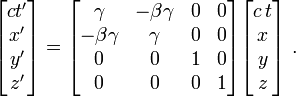
�䤤 β �O v / c �C
Vectors should be transformed same way under same corrd. systems.
�s���ʶq�P��q����
�ʶq
���A�O p = m v �A�ӬO
p = γ m u
�䤤 u �O�Y�[��̬ݨ쪺�t�סA�� m �û������O�R���q�C�o�˩w�~�ມ���ʶq�����w�ߡ]�p�ʶq�u���^�b�۹�פ���Ҧ��[��̩w�ߤ��ܡC
Halliday �ҥ��Ъk�p�U�G�ݭ��s�w�q�ʶq�A�H�ϰʶq�u���w�߾A�ΩP�۹�t�ת��[��̡G
p = m × �[��̮y�Шt�����Z�� / �R��y�Шt�����ɶ� = m Δx / Δt0
�O
�O�����T�����O
F = d p / d t
�]����A�� F = m a�A�Y�Ϧ��ҿת��۹�ʽ�q mr�A�]���ઽ���� mr �N�J F = mr a �AGiancoli �m�{�^
�] ������@�w�n�o�˩w ? �� 4-vector, 4-velocity, 4-momentum �@�����s <���̳Q�n�D���� �ҭۯ� / ���i�Ҵ��� �ഫ> �N�ܲM�� �^
��q
���u�Ҽ{�ʯ�]���b���L���^�A���ӬO 1/2 m v2�A���b�۹�פU�A�ʶq�w�q�w�g���P�A
��q����������
W = ∫ F dx = ∫ dp/dt dx
�䤤 dp / dt = d(γm u) / dt = m/[(1 - v2/c2)(3/2)] dv/dt
�]�n���L�{������ʬ� �s���A�䤤�Q�ΤF �|���ʶq �����ܩʡ^

�\�аʯ�w�z�~��A�ΡA�Y ΔK = W �A�h�o
K = (γ-1) m c2
�G
E = γm c2
�W�� E �O�۹�פU���`��
�ʶq�Я�q���Y
�D�۹�פU E = p2 / 2m �A�b�۹�פU
�ѩ� E = γm c2 �Bp = γm v�A�Ӧ�
E2 = p2 c2 + m2 c4
�Ъ`�N�o�Ӧ��l���S�� γ�Bβ ���۹�t�צ������q�A�W���O�@�Ӻ������ܩʪ���{���C�䤤
m2 c4 = E2 - p2 c2 �� m2 = (E / c)2 - p2 �O�@�Ӯy���ഫ���ܶq�C
�̦��W�����z����
�W�� E2 = p2 c2 + m2 c4 �A�b�R����A�]�ήy�Шt�^ v = 0 �A�G p = γm v = 0
�o E2 = m2 c4�A�Y
E = m c2
E = m c2 �̦��O���o�쪺�H
�R�]���Z�̦��o�{�o���Y�����p�A�O���L�g�U �۹�װʯ�A�ӭn�D���t�����p����t�ɡA���ӭn�ݨ� (1/2) m v2 �����y�O�ǧΦ��C�L���T�O���ݨ�A���o�٦h�F�@�ӻP��q�������`�ƶ� mc2 �C ���z���̦��W��������O�Q�o�{�C
�H�U�i�}�����A
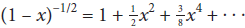
�M�Φb γ �P β �����Y���A �b β �ܤp�����p�U�Aγ �i�H�����
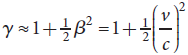
�R�]���Z�b�M�D��o�۹�פ���q�]�ʯ�^���ɡA�ǥѦҼ{�C�t�U�ʯ����ӭn���{ 1/2 m v2 �����G�A �o�{���ݴ�h�@�ӱ`�ƶ� m c2 �~�i�o��A
�����p�U�G
�ʯ� K = (γ - 1) m c2 = m c2/ √[1 - (v/c)2] - m c2
�� v << c �ɡA ���Ǯi�} γ= 1 + 1/2 β2
���ҡG���Ǯi�} γ= [1 - β2](-1/2) = 1 + (-1/2) [1 - 0](-3/2) (-1)β2 + ... = 1 + 1/2 β2 + ...
�ĥμƾǡ]�X��^���y���G��ɶ��b
��ʤ@�V�q����O���A�u�O�ѦҮy�Ъ����P�C���y�ܻ��A��̳��R��A�u�O�U�ۮy�Шt��V�w�줣�P�A�h�@�ӱ���N�i�H�������p�_�ӡC
�ܩ۹�t�ת��ɭԡA�Y�O�t�ץi�����[�������Q���ɪšA�h�u�O�@ x' = x + vt �o�حק�Ӥw�C�M�ӡA�{�b�ڭ̪��D�A�n�������|�Y�u�����Ӥ~�O�ŦX�۹�ת��n�D�C�ڭ̥����n�Ħ�@�طs���ഫ�覡�A�~��{���X�������Y�ήɶ�����]���ȡ^�o�Dz{�H�C
�o�N�ɭP�F�w�q ���i�Ҵ��� (Mikowski) �Ŷ��A�� Lorentz �ഫ���춥�N���F�ӪŶ������@�ر���C����ʬ�W���M�����i�@�B�����Ghttp://en.wikipedia.org/wiki/Introduction_to_special_relativity
�b�w�q�F Minkowski �ɪŤ��� "�Z��" �O s2 = (ct)2 - (x2 + y2 + z2) �����ΤU�A�ݫ�˪��ഫ���b���@�s�Z���w�q�U���b��Ӥ��P�t�ת��[��̦Ө��A�ӶZ�����O���ܪ��A�h�۵M�N�|�ɥX Lorentz �ഫ�����C
Roger Penrose ���O Minkowski �ɪš]spacetime�^���[�����X����A�R�]���Z�۹�ת��[�c�~�⧹���A�i���䭫�n�ʡC
�ҥH�Ŷ��C���O�T���٬O�|�סH�]������t�H�^
���b����_��Ž�W������
���b�ୱ�W�����ơ]�鮩�쥭���W���G����ʤ����Ӫ��D���ҳB���O�����s�@�ɡ^
���b���䩥���_�����p���]�i�H�P�������A���q���ા�D�Ӷ��q�T�w���@��@�W�ӡC�^
�H���@�ɤ���C�]���ڭ̦ۤv���ʪ��t�פ�_���t�Ө��ܺC�C
�ɶ��B�Ŷ��F��l����B��ɱ���
�p�G�Ŷ�����ɱ���i�H�O�L��ɱ���]�S����t�^�A�ɶ��]�i�H���Ŷ������s�_�ӶܡH
���Υ����t�ר���S�O�ܡ]�o���O��N���z�A���O���e���D�^
���쩳�O����F��H
��ӥ��t�O���ɪŵ��c���@�����C
���F��P�����������Y�H
��l������l�ֻP�q�l�����A�O�q�ϧ@�ΤO�����b�@�_���C
���������L���Ҧ��F��t�פ��O���t�B�B�]���T�w�H
��L�F�観��q�A��t���ʯ�өw�C
�O���O�Ҧ��L��q���F��]�ɤl�^���u���@�سt�סA�N�w�O���t�H
�ھڬ۹�ת��n�D���T�����o�ˡ]�Q�Q��q�W�[�������^
���]�R��^��q�O����H
�O�ӦۻP�Ʈ洵�ɤl�椬�@�ζܡHLHC �j�l�R�� 2009 �~�ҥΡA�Q�䵪�ת��Ĥ@�ӽu���]�ɤl�H���^�C
�U�q�۹�ת��L�һP����
beta-�g�u�b�ϳ����s�骺���סA�P��q (��"�ʶq"����) ����
�����W�������o��a�W�C
���y�ìP�w��ͲΡ]�ìP�ɯ�^�� GPS�@��l��
��l�ت�����t���q�l
�۹�q�l�O�ǡйq�l�۱۪��o��
http://library.thinkquest.org/27608/scripts/aview.php3?id=40
�U�ئ��쪺����
�۹�ת����G�ѩ�P�H�̤�`�ͬ��g�禳�t�Z�A�]�Ӥo�F�[���W�ݦ��٬ު� "����"�]�ҿת�thought experiment�^�G
Twin paradox
���M�L�@�Ӧb�a�y�@�ӭ����b�h�Ȧ�A....
�٬��I�G�Ӫš]���t�^�Ȧ�^�ӡA��ӳ����t�~���A�٬ޡC
�����G���ӪŲ�A�n���^�Ӫ����@�Ӹ��~���A���O�q�a�y�[�I�P�ӪŲ�y�[�I�Ҧp���C
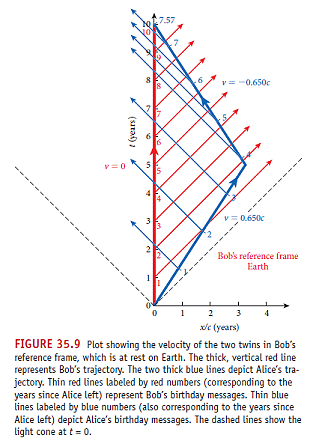
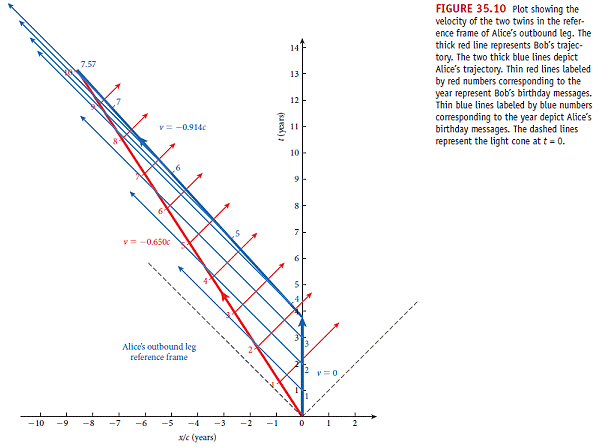
���[�����A�W���o�i�ϫ��ݡH��ӭn�I�G
(1) �ɪŸ��|�W���~���ɶ��y��סA�u�P�ӽu���ײv�����A �V�h�ɶ��y�ʶV�C�C
(2) -0.914c �����l�t�סA�z�L�t�ۥ[�����A���y�� 0.65 �����ĪG�C
Ladder paradox (barn-pole paradox)
 �@�@�@�@�@
�@�@�@�@�@
http://en.wikipedia.org/wiki/Ladder_paradox �]�n�`�N�P�ɩʬO�۹�ӫD���諸�^
(�t�~�A���s�b������� �o�B�P�ϧڭ̭��s�{�� "����" �P "�Ŷ�" ���������Y)
�q�P�Ϫ��i�@�B���Y
�q�y���ͺϤO�A�]�i�ݦ��q�����t�צӾɭP�ҭۯ��Y�u�A�K�״����ҾɭP���q�O! �]�ϴN�O�q�^
�]���R��y�Шt�ݨ쪺�ϲ{�H�������H�a�q�骺���ਤ�ʶq�C�^
�U�q�۹�ת��q������
�ɶ����ȻP�����Y�u���ʵe�t��
http://www.phys.unsw.edu.au/einsteinlight/jw/module4_time_dilation.htm
Open Source Physics �W���ܦh JAVA �g�������z�[������|���ʵe�����A�䤤�]���@�ǬO����۹�ת��A�j�a�i�H�����ݡC
�����W���귽
http://www.phys.unsw.edu.au/einsteinlight/index.html
�s�q�۹�סG���O�]��q�^�P�ɪ� [����²��]
�D�ڴX��]�Ω�y�z���O���Z���Ŷ��^
�L���X��]�������O���ƪ��ܤơA���O�i�ϥηL�������X�ɨ��ˡ^
�Ŷ����q
�q metric �O�N�V�q�D�X���Ȫ���l�A�p�G�סB�T�ڤ�Ŷ����O²�檺���x�} I�C���O�i�q���Φ��]���S�s metric tensor�C
�]���I�����|�̵u�����A�O���u�^
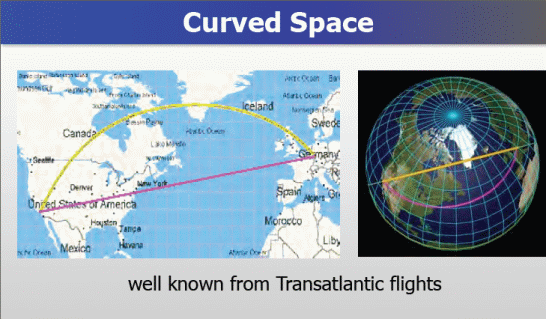
�T�������M�]���A�O 180 ��
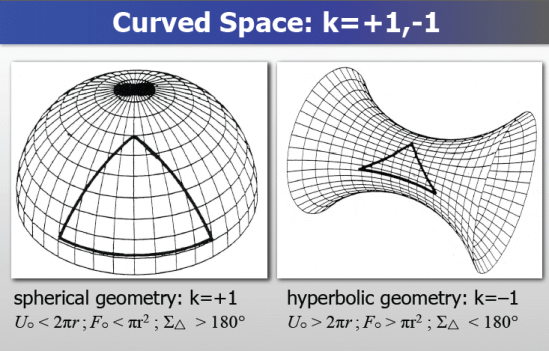
�|�����T�w�Z���A�V����|���^��A��V�]�P�A�o�O���Z�Ŷ��C�]�T���N��^�ӤF���d�ҡ^
���n���T���O�A�����{�b�j�ثפW�P���Z�Ŷ����t���A�Ӥp�d���O���Z���C
���߲z�סG
�@�B��q�N�y���ɶ��Ŷ��s��
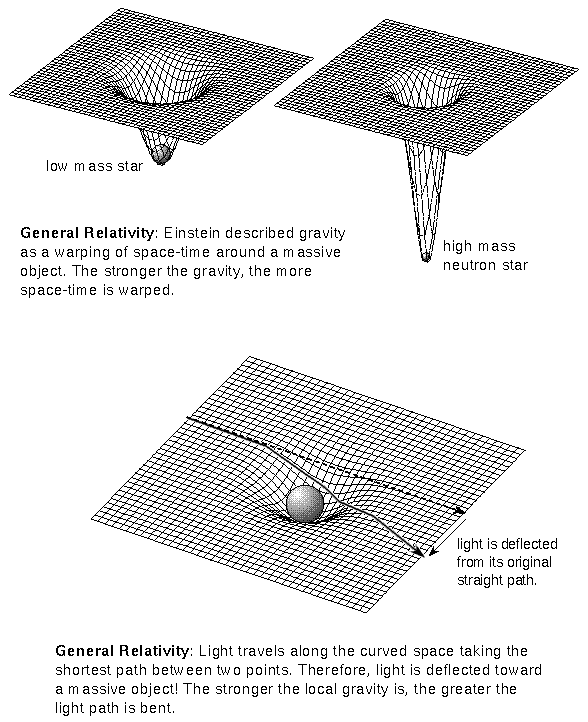
�G�B���O�y���P�y�Шt�B�ʳy�����[�t�O���Ī�
���y���U���ޤO������ĪG�O�����o�͡B���ר⪫�۶Z�h���A�o�O�����H�Ϭ۹�ת��C
���y����"���O"�O���s�b���C���A���O�Y���s�b�A��ī�G���U�Χ��y�Ե۪��ĪG�O����H
�R�]���Z�D�i�A�U�C���k��ت��p������q�y�A���S������~�O�A��̳����b�i��D�ʹB��]���t���u�A�R��]��^�C
���ݥk�ϡA�y��P�~�ɵL��IJ�]�����O�A���ѩ���b�V�W�[�t�������Y�A�����[��̲��ͤF�@�Ӳy��V�U�[�t����ı�A���y��å�������O�A�ӥB�O�H�D�ʤ覡���t���u�B�ʡC�o�@�I�A�b���~���ڭ̬ݱo�D�`�M���C
���U�Ӭݥ��Ϥ��a�y���q�y���v�T�A�R�]���Z���ٲy�������O�ӬO�ȴ`�D�ʪ��W�h�ӹB�ʡC�u���L���ɲy��Ҧb���Ŷ����a�y��q���v�T���s���A�H�P���D�ʹB�ʦb�ڭ̬ݷ|���[�t�ת�"���H"�C
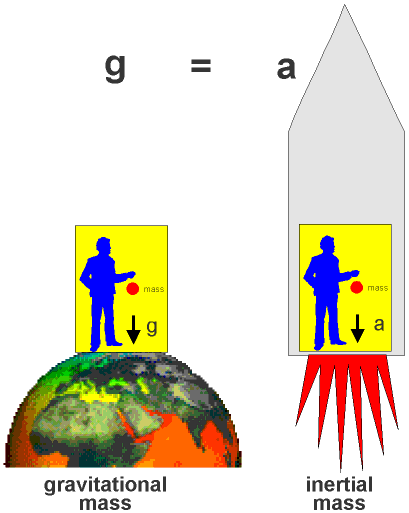
Q : �Ŷ��J�M�s���A������ڭ̶��ۤ�y�����y�e�X���a�y����y��A���i�ݱo�X�O�@�Ӧ��u�ӫD���u�H
A : ���O�̵u�Z���u�A �b�X��ǤW�S�٬����a�u (geodesic line)�C
�s�q�۹�ת��L��
���P����I (perihelion) �i��
����O�i�ʡH
���O�z��
�z���O�B���b�Ӷ��I�᪺����(���P)���٬ݱo��]�ݭn�Q�Τ�k���[��^�A�R�B�y��h 1919 �~�զ���k�[��Ψ쨪�D����h������k�ӱo�H�T�{�A�s�骺���ײŦX�R�]���Z���w���A����������y���Ȫ��Y���C�]�o�Ӳ{�H��¬}�]�A�ΡC�^

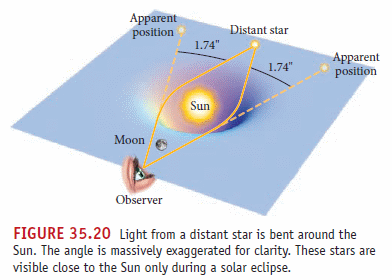
���O���첾�]�Ԩ��Ghttp://zh.wikipedia.org/zh-tw/���O�����^
�ѩ� "�ޤO�ɶ�����" �A�Ӧۭ��O���j���a�誺���u�A�b���O���p���ϰ�Q�[���A�W�v�ܤp�i���ܪ��A�]�����O�j���a��ɨt���C���t�G�C
��ԲӪ���ƥi�� http://en.wikipedia.org/wiki/Tests_of_general_relativity
�{�b�̷Ǫ����A�i����
�W�U�G�Q����
�[���쭫�O�i
LIGO ����A���F 3200 �������_�A���A�q�쭫�O�i�C
Gravity Probe B �p�e�q�� �a�y�P�ɪŦ��v
�Q�Υ|�Ӫ�����
���a�u�]��l�Ŷ��ө��O���u�A�������צӨ��o�O���u�A�A�X�@�y�С^�C
https://zh.m.wikipedia.org/zh-tw/%E5%BC%95%E5%8A%9B%E6%8E%A2%E6%B5%8B%E5%99%A8B
�ɶ�����l���� �P �Ŷ�����ɱ���
�N���� "�ɶ�²�v (A Brief History of Time)"
�ޤH�J�Ӫ��ѦW�]���v�H�ɶ����y�жb�A�p��ͮɶ������v�H�^
�S����ɪ���ɱ��� vs �S����l����l����
�p�G�ɶ��P�Ŷ��O�@�骺�A����ɶ� ...
(�t�@�����G�����������������)
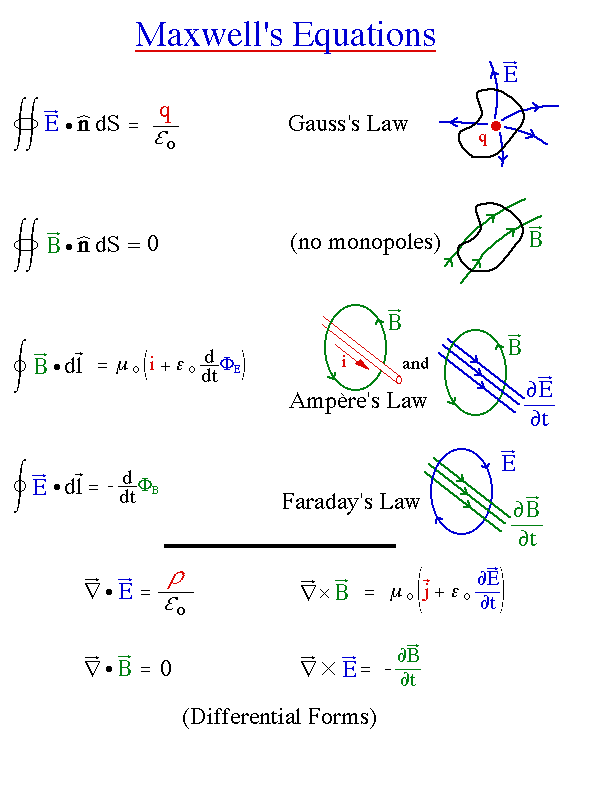





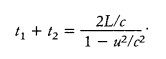 ��
�� 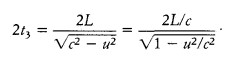 �A���̬O���@�˪��C
�A���̬O���@�˪��C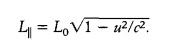
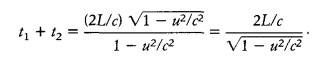





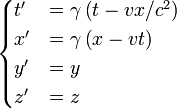
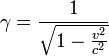
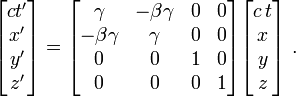

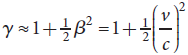


 �@�@�@�@�@
�@�@�@�@�@






